工作多年之后回顾经典排序算法

本文最后更新于：2022年11月4日 凌晨

排序都要做的事情是比较和交换

稳定排序：排序前后，两个相等的元素在其序列中的前后位置顺序相同

这里只有插入排序和归并排序是稳定排序

以下示例均假设我们要从小到大进行排序

选择排序

非稳定排序

排序效率和输入无关

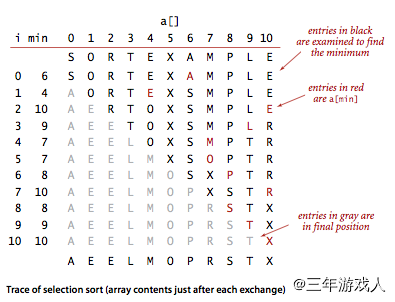
选择排序的基本步骤：先找出最小元素放到0号位置，再找出次小元素放到1号位置，再找出次次小元素放到2号位置，以此类推

排序过程中的数据变化
排序过程图形化

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#ifndef __SELECTIONSORT_H__
#define __SELECTIONSORT_H__

class Selection
{
public:
	//选择排序
  void Sort(char *a, int length)
  {
    for (int index = 0; index < length - 1; ++index)
    {
      //找出从当前位置index开始到后面所有元素中最小元素的下标
      int indexOfCurMin = index;
      for (int i = index + 1; i < length; ++i)
      {
        if (a[i] < a[indexOfCurMin])
        indexOfCurMin = i;
      }

      //将找到的最小元素和index位置上的元素进行交换
      int temp = a[index];
      a[index] = a[indexOfCurMin];
      a[indexOfCurMin] = temp;
    }
  }
};

#endif

特性

该算法的优点是对输入数据的移动次数最少。缺点是运行效率低，无法处理大规模的数据 ## 性能分析 使用该算法对n个元素进行排序时

时间复杂度为O(n^2)，需要对元素进行n(n-1)/2次比较以及n-1次交换。值得注意的是，元素交换次数与元素个数成线性关系，这是其它排序算法都没有的

空间复杂度为0

插入排序

稳定排序

排序效率和输入有关，当待排序的元素越有序（倒置很少）时，该算法可能比其它任何算法都要快

插入排序的基本步骤：每一次都将一个未排序的元素插入到已经排好序的数组中

排序过程中的数据变化
排序过程图形化

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#ifndef __INSERTIONSOER_H__
#define __INSERTIONSOER_H__

//插入排序
class Insertion
{
public:
  void Sort1_0(char *a, int length)
  {
    for (int index = 1; index < length; ++index)
    {
      for (int i = index; i > 0; --i)
      {
        if (a[i] < a[i - 1])
        {
          char temp = a[i];
          a[i] = a[i - 1];
          a[i - 1] = temp;
        }
        //else
        //  break;
      }
    }
  }
  
  //优化版本
  void Sort2_0(char *a, int length)
  {
    for (int index = 1; index < length; ++index)
    {
      char needToInsert = a[index];
    
      int i;
      for (i = index - 1; i >= 0 && needToInsert < a[i]; --i)
        a[i + 1] = a[i];  //右移
    
      a[i + 1] = needToInsert;
    }
  }
};

#endif

特性

这里需要补充两个概念

倒置：两个待排序元素的排列顺序与目标顺序相反

部分有序：如果元素倒置的数量小于元素个数的某个倍数时，那么就说这些待排序元素是部分有序的

该算法缺点是运行效率低，无法处理大规模的数据

插入排序和冒泡排序很像，冒泡排序的算法如下：从未排序元素的第一对直到最后一对，如果第一个元素比第二个元素大就交换，重复这个步骤直到所有元素都排序完成

性能分析

使用该算法对n个元素进行排序时

时间复杂度在最坏的情况下为O(n2)，最好的情况为O(n)，所以平均为O(n2)。元素间的比较次数大于等于倒置数，小于等于倒置数+数组大小-1，在最坏的情况下为n(n-1)/2次，最好的情况下为n-1次。元素间进行交换的次数等于倒置数，在最坏的情况下为n(n-1)/2次，最好的情况下为0次

空间复杂度为0

希尔排序

非稳定排序

排序效率是否输入有关取决于第二步使用的排序算法是否输入有关

希尔排序的基本步骤： 1. 确定h的初值 1. 每次循环都使数组中任意间隔为h的元素都是有序的（这样的数组称为h有序数组） 1. 每次循环结束，h都要递减一次，直到h等于1

ps：h的递减方式是多种多样的，不同的递减方式决定了希尔排序算法的效率，目前还没有研究出最好的递减序列

递减序列的一个例子
排序过程图形化

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
//基于插入排序的希尔排序算法
#ifndef __SHELLSORT_H__
#define __SHELLSORT_H__

//希尔排序
class Shell
{
public:
  //1.0版本
  void Sort1_0(char *a, int length)
  {
    //确定h的最大值
    int h = 1;
    while (h < length / 3)
      h = 3 * h + 1;    //1,4,13,40,121,364,1093，...
  
    while (h >= 1)  //间隔控制
    {
      for (int i = 0; i < h; ++i)  //每个子数组的头
      {
        //对每个子数组进行插入排序
        for (int j = i + h; j < length; j += h)
        {
          char needToInsert = a[j];
          int k;
          for (k = j - h; j >= i&&needToInsert < a[k]; k -= h)
            a[k + h] = a[k];
      
          a[k + h] = needToInsert;
        }
      }
    
      h /= 3;
    }
  }
  
  //2.0版本
  void Sort2_0(char *a, int length)
  {
    //确定h的最大值
    int h = 1;
    while (h < length / 3)
      h = 3 * h + 1;    //1,4,13,40,121,364,1093，...
  
    while (h >= 1)
    {
      for (int i = h; i < length; ++i)    //从所有子数组的第二元素开始到最后的元素，妙
      {
        //在i元素所属的子数组内对i元素进行插入排序
        char needToInsert = a[i];
        int j;
        for (j = i - h; j >= 0 && needToInsert < a[j]; j -= h)
          a[j + h] = a[j];
    
        a[j + h] = needToInsert;
      }
    
      h /= 3;
    }
  }
};

#endif

特性

该算法的优点是可以处理大规模的数据，适用于大部分场合，其它更复杂优秀的排序算法最多比该算法快2倍。缺点是无法处理超大规模的数据

性能分析

使用该算法对n个元素进行排序时

时间复杂度目前在数学上是未知的

空间复杂度为0

归并排序

稳定排序

排序效率与输入无关

归并效果
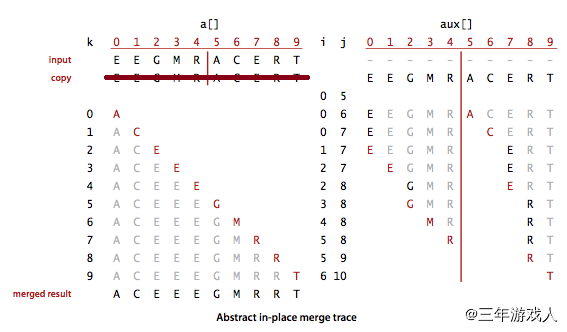
归并过程中的数据变化
自顶向下的排序过程中的数据变化
自顶向下的排序过程图形化
自底向上的排序过程中的数据变化
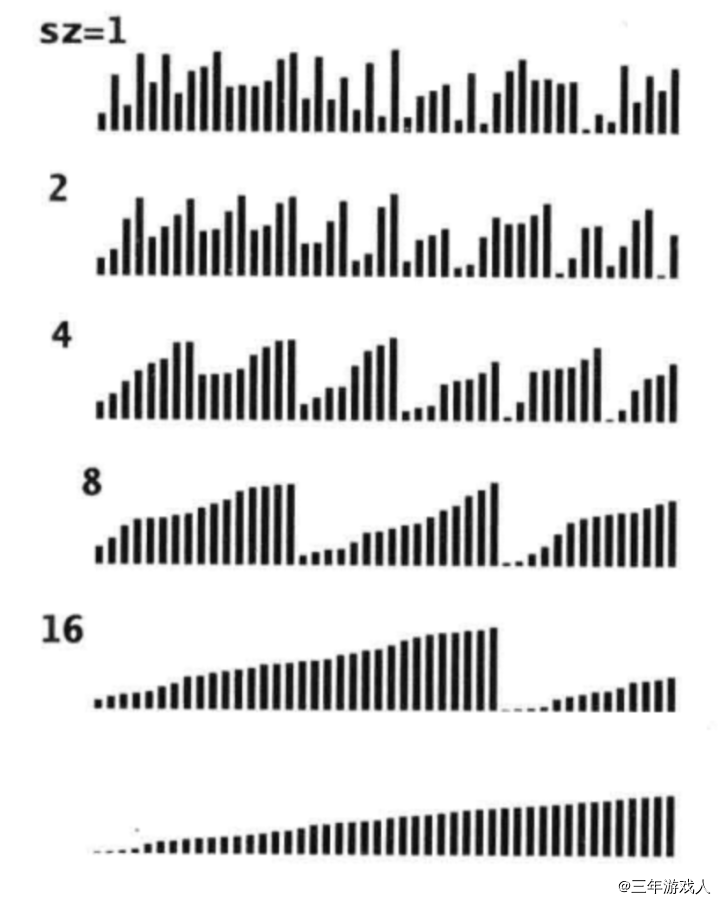
自底向上的排序过程图形化

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
#ifndef __MERGESORT_H__
#define __MERGESORT_H__

#include <iostream>  /* NULL */
#include <algorithm>  /* min */

using namespace std;

class Merge
{
private:
  //原数组的副本,辅助空间
  char *aux;
public:
  Merge(){ aux = NULL; }
  
  //单次归并，将a数组的两部分已排好的子数组合并起来
  //mid代表左边子数组的最后一个元素下标
  void merge(char *a, int left, int mid, int right)
  {
    for (int i = left; i <= right; ++i)
      aux[i] = a[i];
  
    int idxOfLeft = left;
    int idxOfRight = mid + 1;
    //开始归并
    for (int i = left; i <= right; ++i)
    {
      if (idxOfLeft > mid&&idxOfRight <= right)
        a[i] = aux[idxOfRight++];
      else if (idxOfLeft <= mid&&idxOfRight > right)
        a[i] = aux[idxOfLeft++];
      else if (aux[idxOfLeft] < aux[idxOfRight])
        a[i] = aux[idxOfLeft++];
      else
        a[i] = aux[idxOfRight++];
    }
  }
  
  //自顶向下的递归归并排序
  //这个函数还可以优化，如果left和right之间的插值小到一定的程度，就不用再递归了；直接用插入排序、希尔排序或者选择排序，速度可以提升；其中插入排序可以缩短10%~15%
  void SortCore(char *a, int left, int right)
  {
    if (left >= right)        //可以改成==
      return;
    else
    {
      int mid = (left + right) / 2;
      SortCore(a, left, mid);
      SortCore(a, mid + 1, right);
      merge(a, left, mid, right);    //这条语句在执行前还可以做一个判断：如果a[mid]<=a[mid+1]，这条语句可以不执行；
    }
  }
  
  //启动函数
  void Sort(char *a, int length)
  {
    //防止内存泄漏
    if (aux != NULL)
    {
      delete[] aux;
      aux = NULL;
    }
  
    aux = new char[length];
    SortCore(a, 0, length - 1);
  }
  
};

class MergeBu
{
private:
  //a数组的副本,辅助空间
  char *aux;

public:
  MergeBu(){ aux = NULL; }
  
  //单次归并，将a数组的两部分已排好的子数组合并起来
  //mid代表左边子数组的最后一个元素下标
  void merge(char *a, int left, int mid, int right)
  {
    for (int i = left; i <= right; ++i)
      aux[i] = a[i];
  
    int idxOfLeft = left;
    int idxOfRight = mid + 1;
    //开始归并
    for (int i = left; i <= right; ++i)
    {
      if (idxOfLeft > mid&&idxOfRight <= right)
        a[i] = aux[idxOfRight++];
      else if (idxOfLeft <= mid&&idxOfRight > right)
        a[i] = aux[idxOfLeft++];
      else if (aux[idxOfLeft] < aux[idxOfRight])
        a[i] = aux[idxOfLeft++];
      else
        a[i] = aux[idxOfRight++];
    }
  }
  
  //自底向上的归并排序
  //可以给链表进行排序，而不用辅助数组
  void Sort(char *a, int length)
  {
    //保险
    if (aux)
    {
      delete[] aux;
      aux = NULL;
    }
  
    aux = new char[length];
  
    for (int subArraySize = 1; subArraySize < length; subArraySize <<= 1)
    {
      for (int left = 0; left + subArraySize < length; left += (subArraySize << 1))    //注意这里的终止条件
        merge(a, left, left + subArraySize - 1, min(left + (subArraySize << 1) - 1, length - 1));
    }
  }
};

#endif

特性

该算法的优点是能够处理超大规模的数据，缺点是需要O(n)大小的辅助空间

性能分析

使用该算法对n个元素进行排序时

时间复杂度为O(nlgn)，元素间的比较次数在最坏的情况下为nlgn次，在最好的情况下为(nlgn/2)次，平均为(nlgn)(3/4)次。

空间复杂度为O(n)+递归辅助栈大小

快速排序

非稳定排序

在介绍算法之前需要先了解一个操作--切分

切分的目标是通过调整数组将首元素(或尾元素)放到正确的位置。该位置左边的元素都小于该位置的元素，右边的元素都大于该位置的元素。切分的一个经典应用是查找数组中第k大的元素。需要注意的是，切分要在一个数组上进行各种交换操作，如果不想改变原数组的话，则需要多创建一个数组来进行辅助

快速排序函数的基本步骤：对数组进行切分，再对经过切分得到的两个子数组分别调用快速排序函数

切分效果
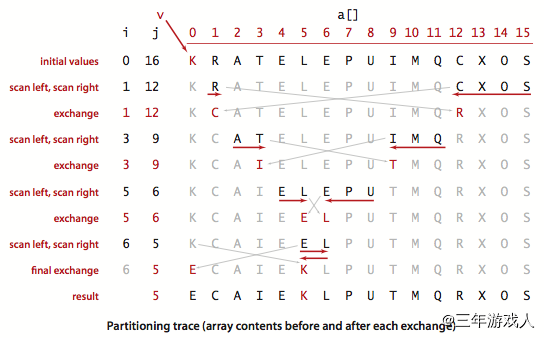
切分过程中的数据变化
排序过程中的数据变化
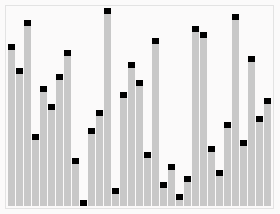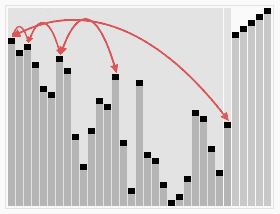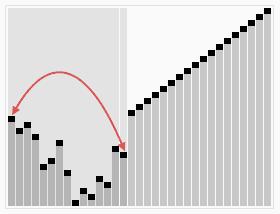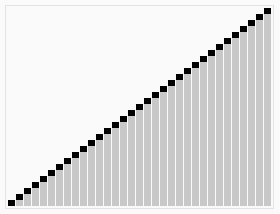
排序过程图形化（每次都用当前数组中的最后一个元素进行切分）

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
#ifndef __QUICKSORT_H__
#define __QUICKSORT_H__

class Quick
{
public:
  void Sort(char *a, int length)
  {
    //在开始递归排序前最好先打乱一下数组，防止不合理的切分；这样就不容易出现O(N^2)这种情况
    SortCore(a, 0, length - 1);
  }
  
  //可以优化：在数组被分割得小于某个数值的时候，改用插入排序
  void SortCore(char *a, int left, int right)
  {
    if (left >= right)
    {
      return;
    }
    else
    {
      int j = Partition(a, left, right);
      SortCore(a, left, j - 1);
      SortCore(a, j + 1, right);
    }
  }
  
  //可以优化：选取部分元素来找出这部分元素的中位数当作基准
  //可以优化（代码看quick3way）  
  int Partition(char *a, int left, int right)
  {
    //分割标准，取了首元素来当标准
    char standard = a[left];

    int i = left+1;
    int j = right;
    while(true)
    {
      //特别注意 ++i 和 --j 的位置
      //注意a[i] <= standard和standard <= a[j]的等于号
      while (i <= right && a[i] <= standard){ ++i; }      //i <= right可以改成i < right
      while (j >= left + 1 && standard <= a[j]){ --j; }    //j >= left+1不可以更改j > left+1
     
      if (i < j)
      {
        char temp = a[i];
        a[i] = a[j];
        a[j] = temp;
      }
      else
        break;
     
    }

    a[left] = a[j];
    a[j] = standard;
  
    return j;
  }
};

//三向切分的快速排序：在一个数组中，不会多次选择主键值同样的元素作为基准；可以改成三向切分，就是比基准值小的元素放在左边，与基准值相等的元素放在中间，比基准值大的元素放在右边；对于包含大量重复元素的数组，可以将时间复杂度有NlgN降到N
class Quick3way
{
public:
  void Sort(char *a, int length)
  {
    //在开始递归排序前最好先打乱一下数组，防止不合理的切分；这样就不容易出现O(N^2)这种情况
    SortCore(a, 0, length - 1);
  }
  
  void SortCore(char *a, int left, int right)
  {
    if (left >= right)
    {
      return;
    }
    else
    {
      //三向切分
#if 0
      //第一次切分
      char standard = a[left];
      int i = left+1;
      int j = right;
      while(true)
      {
        while (a[i] < standard && i <= right){ ++i; }
        while (standard <= a[j] && j >= left+1){ --j; }
    
        if (i < j)
        {
          char temp = a[i];
          a[i] = a[j];
          a[j] = temp;
        }
        else
          break;
      }
      a[left] = a[j];
      a[j] = standard;
    
      int lessRight = j - 1;
    
      //第二次切分
      j = right;
      while(true)
      {
        while (a[i] == standard && i <= right){ ++i; }
        while (standard < a[j] && j >= lessRight + 2){ --j; }
    
        if (i < j)
        {
          char temp = a[i];
          a[i] = a[j];
          a[j] = temp;
        }
        else
          break;
      }
    
      int equelRight = j;
    
      SortCore(a, left, lessRight);
      SortCore(a, equelRight + 1, right);
#endif
#if 1  
      //如果无法理解这段代码，请使用样例：6、2、3、7、6、6、9、1，来模拟一下
      char standard = a[left];
      //[left,lt-1]中的元素都小于基准值
      //[lt,i-1]中的元素都等于基准值
      //[gt+1,right]中的元素都大于基准值
      int lt = left;
      int i = left + 1;
      int gt = right;
      while (i <= gt)
      {
        if (a[i] < standard)
        {
          char temp = a[i];
          a[i] = a[lt];
          a[lt] = temp;
      
          ++i;
          ++lt;
        }
        else if (a[i] == standard)
        {
          ++i;
        }
        else if (a[i] > standard)
        {
          char temp = a[i];
          a[i] = a[gt];
          a[gt] = temp;
      
          --gt;
        }
      }
      
      SortCore(a, left, lt - 1);
      SortCore(a, i, right); 
#endif
    }
  }
};

#endif

特性

该算法的优点是可优化的空间大，经过精心调优的快速排序在大多数情况下都会比其他基于比较的排序算法更快，缺点是如果每次切分选择的元素都不正确，算法运行效率就会大幅度降低。例如第一次选了最小元素，第二次选择了次小元素作基准...，这种情况下时间复杂度就会变成O(n^2)，但是这种情况出现的概率比你电脑被雷劈中的概率还要小

性能分析

使用该算法对n个元素进行排序时

时间复杂度为O(nlgn)，虽然和归并排序一样，但是比归并要快

空间复杂度为递归辅助栈的大小

优先队列

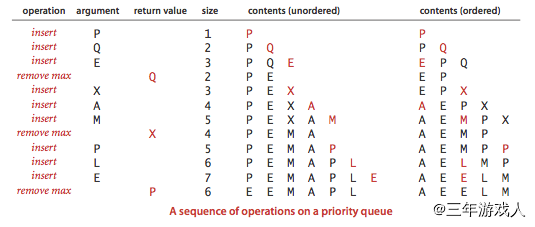
在讲解堆排序之前需要先介绍一个数据结构--优先队列。该数据结构每一次取元素都只能获取最大（或最小）的元素

实现优先队列的方式有很多种

可以通过数组来实现无序或有序的优先队列

还可以通过二叉堆来实现。二叉堆是一棵父节点总是大于（或小于）等于两个子节点的二叉树，这样一棵二叉树又可以说是堆有序的。二叉堆可以使用数组形式的完全二叉树来存储

树包括堆，堆包括二叉堆。因为一般使用的堆都是二叉堆，所以通常将二叉堆称为堆

为堆添加或移除元素都会先破坏堆的有序状态，然后再遍历堆来恢复有序状态（这个过程称为堆的有序化） ## 基于二叉堆实现的优先队列 以下二叉堆都是最大堆

上浮过程（插入操作的基础）
下沉过程（删除操作的基础）
插入元素（左）、删除元素（右）的过程

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
//优先队列的一种实现方式：二叉堆
//二叉堆：用这个数据结构可以很容易进行排序，但是直接用这个数据结构来排序效率并不高，因为我们只用很小一部分代码就够了
class MaxPQ
{
private:
  char *pq;    //节点为k，父节点为(k-1)/2，左孩子为2*k+1，右孩子为2*k+2
  int count;   //记录堆中元素的个数
public:
  MaxPQ(int maxN)
  {
    pq = new char[maxN];
    count = 0;
  }
  ~MaxPQ()
  {
    delete[] pq;
  }
  bool isEmpty()
  {
    return count == 0;
  }
  int size()
  {
    return count;
  }
  void insert(char v)
  {
    pq[count] = v;
    swim(count);

    ++count;
  }
  char delMax()
  {
    char max = pq[0];

    char temp = pq[0];
    pq[0] = pq[count - 1];
    pq[count - 1] = temp;

    --count;

    sink(0);

    return max;
  }
  //核心
  void swim(int k)
  {
    while (k > 0 && pq[k] > pq[(k - 1) / 2])
    {
      char temp = pq[k];
      pq[k] = pq[(k - 1) / 2];
      pq[(k - 1) / 2] = temp;

      k = (k - 1) / 2;
    }
  }
  //核心
  void sink(int k)
  {
    while (2 * k + 1 < count)
    {
      int maxChild = 2 * k + 1;
      if (maxChild + 1 < count && pq[maxChild + 1] > pq[maxChild])
        ++maxChild;

      if (pq[k] >= pq[maxChild])
        break;
      else
      {
        char temp = pq[k];
        pq[k] = pq[maxChild];
        pq[maxChild] = temp;

        k = maxChild;
      }

    }
  }
};

性能分析

数据结构 插入第一个元素 删除最大元素
基于有序数组的优先队列 N 1
基于无序数组的优先队列 1 N
基于二叉堆的优先队列 lgN lgN
某种理想的优先队列 1 1

从N个元素中找到最大的M个元素所需的成本：

某种理想的优先队列 时间复杂度 空间复杂度（用于存储N个输入）
其他最快的排序算法 NlgN N
数组实现的优先队列 NM M
二叉堆实现的优先队列 NlgM M

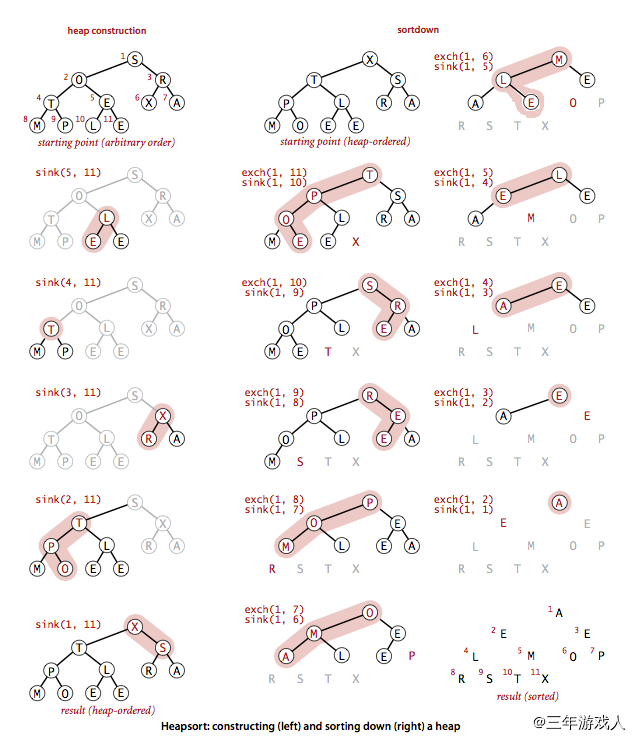
堆排序

非稳定排序

堆排序的基本步骤： 1. 将一个数组建成堆，建堆的方法有两种： 1. 层序遍历二叉树（从左到右遍历数组），每个节点都进行上浮操作 2. 从非叶子节点开始反向层序遍历二叉树（从右到左遍历数组），每个节点都进行下沉操作。这种方式的效率更高，只需要少于2N次比较以及少于N次交换 2. 不断删除堆顶元素

排序过程中的数据变化
排序过程中的数据变化
排序过程图形化

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#ifndef __HEAPSORT_H__
#define __HEAPSORT_H__

class Heap
{
public:
  //注意：count是待排序数组的长度
  void sink(char *a, int k, int count)
  {
    while (2 * k + 1 < count)
    {
      int maxChild = 2 * k + 1;
      if (maxChild + 1 < count && a[maxChild + 1] > a[maxChild])
        ++maxChild;

      if (a[k] >= a[maxChild])
        break;
      else
      {
        char temp = a[k];
        a[k] = a[maxChild];
        a[maxChild] = temp;

        k = maxChild;
      }
    }
  }
  //可以优化：先下沉后上浮，可将比较次数减少一半；这个方法需要额外的空间来辅助，只有当比较需要很高的代价时才采用
  void sort(char *a,int count)
  {
    for (int i = (count - 1) / 2; i >= 0; --i)
      sink(a, i, count);

    for (int i = count - 1; i > 0; --i)
    {
      char temp = a[i];
      a[i] = a[0];
      a[0] = temp;

      sink(a, 0, i);
    }
  }
};

#endif
算法
工作多年之后回顾经典排序算法
https://roudersky.com/posts/1f3756ac.html
作者
Rouder
发布于
2021年12月23日
许可协议