算法题--重建二叉树

6 # 要求 时间限制：1秒 空间限制：32768K

题目描述

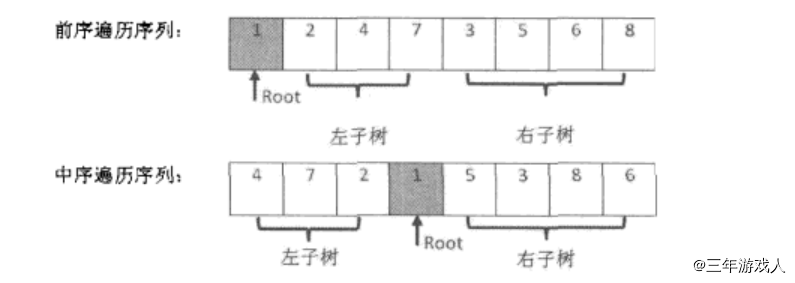
输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建二叉树并返回

解题思路

解题的前提：两个序列中必须有一个中序序列

前（后）序序列用于提供根节点，根节点就是序列第一个元素（最后一个元素）

中序序列用于确定当前根节点的左右子树有哪些节点

如下图所示：

确定了左右子树有哪些元素之后就继续递归

代码

/*
Definition for binary tree
struct TreeNode
{
  int val;
  TreeNode *left;
  TreeNode *right;
  TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
*/
class Solution
{
public:
  TreeNode* reConstructBinaryTree(vector<int> pre,vector<int> vin)
  {
    int psize=pre.size();
    int vsize=vin.size();
      
    if(psize==0 || vsize==0 || psize != vsize)
      return NULL;
      
    return reBuildBinaryTreeCore(pre, 0, psize-1, vin, 0, vsize-1);
  }
  
  TreeNode* reBuildBinaryTreeCore(vector<int>& pre, int startIdxOfP, int endIdxOfP,
                                  vector<int>& vin, int startIdxOfV, int endIdxOfV)
  {
    int valOfRoot = pre[startIdxOfP];
    TreeNode* root = new TreeNode(valOfRoot);
    
    if(startIdxOfP == endIdxOfP)
    {
      if(startIdxOfV == endIdxOfV)
        return root;
      else
      {
        cout << "无效输入" << endl;
  	abort();
      }
    }
    else
    {
      int idxOfRootInV = 0;
      for(idxOfRootInV = startIdxOfV;idxOfRootInV <= endIdxOfV && 
          vin[idxOfRootInV] != valOfRoot;++idxOfRootInV)
      {
      }
      if(vin[idxOfRootInV] != valOfRoot)
      {
        cout << "无效输入" << endl;
        abort();
      }
    	
      int leftLength = idxOfRootInV - startIdxOfV;
      //左
      if(startIdxOfV <= idxOfRootInV - 1)
        root->left = reBuildBinaryTreeCore(pre,
                                           startIdxOfP + 1,
                                           startIdxOfP + leftLength,
                                           vin,
                                           startIdxOfV,
                                           idxOfRootInV - 1);
      //右
      if(idxOfRootInV + 1 <= endIdxOfV)
        root->right = reBuildBinaryTreeCore(pre,
                                            startIdxOfP + 1 + leftLength,
                                            endIdxOfP,
                                            vin,
                                            idxOfRootInV+1,
                                            endIdxOfV);
    }
    
    return root;
  }
};